Mathematics

First of all let me get this out of the way. Math is absolutely not something I'd do for a living. I was a decent math student in school, but never spectacular. But I can't help my insatiable instinct of branching into the esoteric in many subjects. That's why like all of my other interests, I gravitated towards one of the least practical fields in math: theoretical mathematics and number sequences. I suppose it was discovering Numberphile, the YouTube channel that sparked my interest. Through mathematician Neil Sloane's appearances, I discovered the On-Line Encyclopedia of Integer Sequences.

Since then, I've been compiling spreadsheet after spreadsheet trying to find interesting number sequences, especially the primes, which inspired my Prime Finder website. I was looking for a website that found large primes for a letter n for a given formula. Now I can use my tool to find primes that are thousands of digits in length within only a couple minutes. Although I haven't discovered any "massive breakthroughs" in the math field yet, I'm still looking. I'm still looking. A couple formulas I found however, are very rare in producing primes. My next possible project might be looking for formulas that generate a lot of primes in comparison.

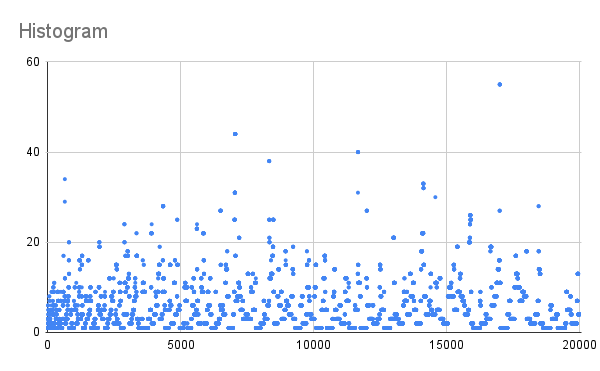In fact, one of my most successful math projects was the prime root sequence, something I submitted to the OEIS for consideration. It got approved (with much alteration of semantics) and you can now find it there under A357477. The sequence has a quite an irregular pattern to it with a seemingly random, unexplained reason behind it at the moment. The other two series related to it describe indices at which record hight numbers in the primary sequence appear (A357675), as well as the first appearance of each ordinal number as it shows up in the sequence (A357676). These other two graphs follow pretty standard logarithmic equations, however, the initial graph is still a bit of a enigma.

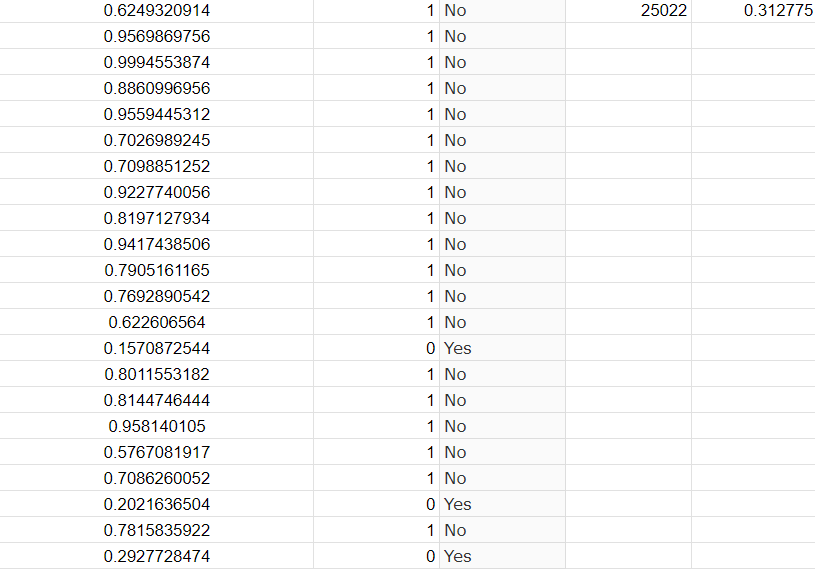Another thing I love is looking for patterns with π and other transcendental numbers such as e and ln2. I have tried to find the best π approximations, and wrote a Python program to help me look for them. The best one I found so far that is easy and compact to write is cuberoot(318) - cuberoot(50), which is accurate to seven digits if you don't round. I've also stumbled upon π when doing unrelated things. I made a program that generates random numbers from 0 to 1 on a spreadsheet and then creates a giant power tower of them about 80,000 times. And then I count what percentage of the resulting numbers can be rounded to one. It turns out that this series tends to about 0.31415, I've conjectured or π/10.